了解 WormHole 路由中的近似誤差和查詢複雜性
連結目錄
摘要和 1. 引言
1.1 我們的貢獻
1.2 設定
1.3 演算法
-
相關工作
-
演算法
3.1 結構分解階段
3.2 路由階段
3.3 WormHole的變體
-
理論分析
4.1 預備知識
4.2 內環的次線性
4.3 近似誤差
4.4 查詢複雜度
-
實驗結果
5.1 WormHole𝐸, WormHole𝐻 和 BiBFS
5.2 與基於索引方法的比較
5.3 WormHole作為基本元素: WormHole𝑀
參考文獻
4.3 近似誤差
現在我們有了包含Chung-Lu核心的次線性內環,我們必須證明通過它路由路徑只會產生很小的損失。直觀上,內環越大,這一點越容易滿足:如果內環是整個圖,這個陳述就變得顯而易見。因此,挑戰在於證明即使使用次線性內環,我們也能在準確性方面達到強有力的保證。我們證明WormHole對所有點對產生的加性誤差最多為𝑂(loglog𝑛),這比直徑Θ(log𝑛)小得多。
\ 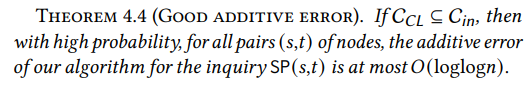
\ 上述結果即使在最壞情況下也以高概率成立。也就是說,對於圖中所有頂點對(𝑠,𝑡),WormHole返回的路徑長度最多比𝑠和𝑡之間的實際距離高出𝑂(loglog𝑛)。這顯然意味著WormHole的平均加性誤差,以高概率被相同的量所限制。
\ 
\
4.4 查詢複雜度
回顧本文中的節點查詢模型(見§1.2):從單個節點開始,我們可以迭代地進行查詢,每次查詢都會檢索我們選擇的節點𝑣的鄰居列表。我們關注的是查詢複雜度,即進行特定操作所需的查詢次數。
\ \ 
\ \ 第一個結果是我們性能的上界。
\ \ 
\ \ 證明概要。對於給定的查詢SP(𝑢, 𝑣),我們給出從𝑢開始的BFS的查詢複雜度上界,對於𝑣也類似;總查詢複雜度是這兩個量的總和。
\ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \ \ 
\ \
:::info 作者:
(1) Talya Eden,巴伊蘭大學 (talyaa01@gmail.com);
(2) Omri Ben-Eliezer,麻省理工學院 (omrib@mit.edu);
(3) C. Seshadhri,加州大學聖克魯茲分校 (sesh@ucsc.edu)。
:::
:::info 本論文可在 arxiv 上獲取,採用 CC BY 4.0 授權。
:::
\
您可能也會喜歡

Ripple 透過 10 億美元收購 GTreasury 進入 120 兆美元企業財資市場

Ethereum 現貨 ETF 昨日總計淨流出 5687.66 萬美元,僅 BlackRock ETHA 出現淨流入
