WormHole 如何加速十億邊緣圖中的路徑尋找

連結目錄

摘要和 1. 引言

1.1 我們的貢獻

1.2 設定

1.3 演算法

1. 相關工作

2. 演算法

   3.1 結構分解階段

   3.2 路由階段

   3.3 WormHole的變體

3. 理論分析

   4.1 預備知識

   4.2 內環的次線性性質

   4.3 近似誤差

   4.4 查詢複雜度

4. 實驗結果

   5.1 WormHole𝐸、WormHole𝐻和BiBFS

   5.2 與基於索引方法的比較

   5.3 WormHole作為基本元件：WormHole𝑀

參考文獻

1.1 我們的貢獻

我們設計了一種新演算法WormHole，它創建了一個數據結構，通過利用許多社交和信息網絡的典型結構來回答多個最短路徑查詢。WormHole簡單、易於實現，並有理論支持。我們提供了它的幾種變體，每種都適用於不同的設定，在各種網絡數據集上展示了出色的實證結果。以下是其一些關鍵特點：

\ • 性能-精確度權衡。 據我們所知，我們的演算法是大型網絡中第一個近似次線性最短路徑演算法。我們允許小的加法誤差，這導致了預處理時間/空間和每次查詢時間之間的權衡，並使我們能夠提出

\

\ 一個具有高效預處理和快速查詢時間的解決方案。值得注意的是，我們最精確（但最慢）的變體WormHole𝐸具有近乎完美的精確度：超過90%的查詢沒有加法誤差，在所有網絡中，超過99%的查詢的加法誤差最多為2。詳情請參見表3。

\ • 極快的設置時間。 即使對於擁有十億條邊的圖，我們最長的索引構建時間也只有兩分鐘。相比之下，PLL和MLL在我們測試的一半網絡上超時，而對於PLL和MLL確實完成運行的中等大小的圖，WormHole索引構建速度快了100倍。也就是說，WormHole在幾秒鐘內完成，而PLL則需要數小時。請參見表4和表5。這種快速設置時間是通過使用次線性大小的索引實現的。對於我們考慮的最大網絡，只需要取約1%的節點作為索引就能獲得較小的平均加法誤差 - 見表1。對於較小的網絡，可能高達6%。

\ • 快速查詢時間。 與BiBFS相比，普通版本的WormHole𝐸（沒有任何基於索引的優化）對幾乎所有圖都快2倍，對我們測試的三個最大圖快4倍以上。簡單變體WormHole𝐻在犧牲一些精確度的情況下實現了數量級的改進：在幾乎所有圖上一致快20倍，對於我們擁有的最大圖快180倍以上。完整比較請參見表3。基於索引的方法通常在微秒級回答查詢；上述兩種變體仍在毫秒級範圍內。

\ • 結合WormHole和最先進技術。WormHole通過存儲一小部分頂點並在其上計算精確最短路徑來工作。對於任意查詢，我們通過這個我們稱為核心的子集來路由路徑。我們利用這一見解提供第三種變體WormHole𝑀，在核心上實現最先進的最短路徑技術MLL。這在設置成本只有一小部分的情況下實現了與MLL相當的查詢時間（具有與WormHole𝐻相同的精確度保證），並且可以在MLL無法終止的大型圖上運行。我們在§5.3中探討了這種組合方法，並在表6中提供了統計數據。

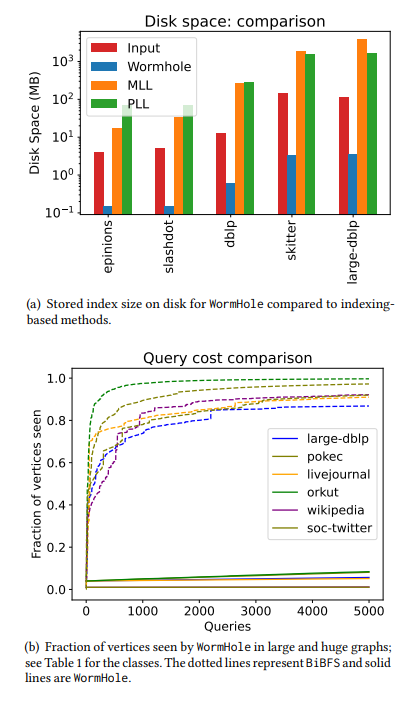
\ • 次線性查詢複雜度。 查詢複雜度指的是演算法查詢的頂點數量。在有限查詢訪問模型中，查詢一個節點會顯示其鄰居列表（見§1.2），我們的演算法的查詢複雜度隨著所做的距離/最短路徑查詢數量而良好擴展。為了回答5000個近似最短路徑查詢，我們的演算法對大多數網絡只觀察了1%到20%的節點。相比之下，BiBFS為了回答幾百個最短路徑查詢，需要查看超過90%的圖。比較請參見圖2和圖5。

\ • 對誤差和性能的可證明保證。 在§4中，我們證明了一系列理論結果，補充並解釋了實證性能。以下非正式陳述的結果是針對具有冪律度分布的Chung-Lu隨機圖模型[15-17]證明的。

\ 定理1.1（非正式）。在具有冪律指數𝛽∈(2,3)的n個頂點的Chung-Lu隨機圖𝐺中，WormHole以高概率具有以下保證：

\

\

:::info 作者：

(1) Talya Eden，巴伊蘭大學 (talyaa01@gmail.com)；

(2) Omri Ben-Eliezer，麻省理工學院 (omrib@mit.edu)；

(3) C. Seshadhri，加州大學聖克魯茲分校 (sesh@ucsc.edu)。

:::

:::info 本論文可在arxiv上獲取，採用CC BY 4.0許可證。

:::

\