No Winners Here: Why Every “Fair” Crypto Auction Ends Up Trivial
Table of Links
Abstract and 1. Introduction
1.1 Technical Overview
1.2 Related Work
-
Model and Preliminaries and 2.1 Transaction Fee Mechanisms
2.2 The TFM Desiderata
-
Understanding OCA
3.1 The Difference Between SCP and OCA
3.2 Useful Preliminary Results for OCA-proof TFMs
-
Deterministic OCA-proof Mechanisms
-
Randomized OCA-proof Mechanisms
-
Discussion and References
\
A. Missing Proofs
B. Non-anonymous Deterministic Mechanisms
4 Deterministic OCA-proof Mechanisms
Example 3.6 shows that generally, the DSIC and 1-OCA-proofness properties are not enough to guarantee zero revenue. We now show that for deterministic mechanisms, adding the MMIC property suffices to get a general 0 revenue result.
\ Theorem 4.1. Every deterministic DSIC+MMIC+1-OCA-proof mechanism has 0 miner revenue.
\ 
\ However, we can provide a meaningful characterization even when removing the DSIC condition. The characterization, given in Lemma 4.3, remains very similar, albeit with more freedom to decide the payment rule.
\ 
\ We conclude that the burn for all allocated values is some constant R. We now compare R with the r we have for the allocation rule.
\ We conclude that R = r, which yields the specified characterization.
\ This allows us to further characterize the allocation and burn rules more generally, for deterministic 1-OCA-proof mechanisms.
\ Lemma 4.4. Any 1-OCA-proof deterministic mechanism a, p, β is exactly of the following form: For some r ≥ 0, the mechanism allocates the item to the highest bidder subject to it having higher value than r, or does not allocate the item at all. Whenever allocated, the burn is exactly r. I.e.,
\ 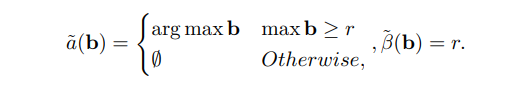
\ 
\ We now can precisely characterize two classes of mechanisms: The class of DSIC+1-OCA-proof deterministic mechanisms, and the class of MMIC+1-OCA-proof deterministic mechanisms.
\ 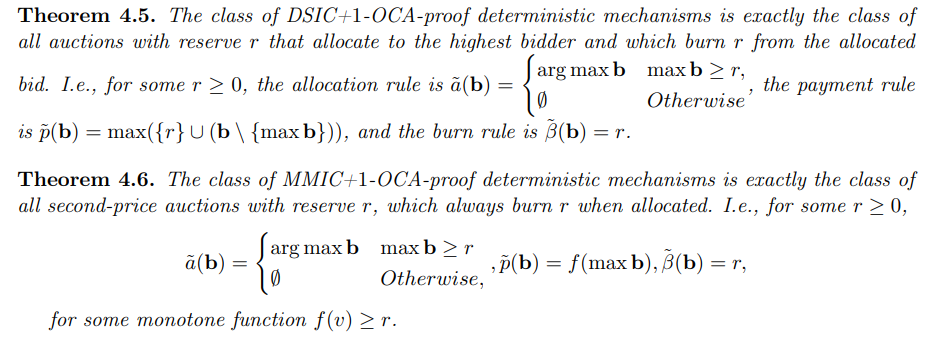
\ These precise characterizations now allow us to conclude with the following:
Theorem 4.7. Never allocating the item is the only DSIC+MMIC+1-OCA-proof deterministic mechanism.
\ Proof. This follows from Theorem 4.5 and Theorem 4.6, as the two classes characterized in these results only have the trivial mechanism in common (taking r = ∞). To intuitively see this, consider the class of second-price auctions with reserve r and constant burn r of Theorem 4.5. Second-price auctions are not MMIC since the miner can add a fake bidder arbitrarily close to the winning bid to increase the payment.
\
5 Randomized OCA-proof Mechanisms
We now extend the discussion to randomized OCA-proof mechanisms. For randomized mechanisms, we consider the stronger notion of OCA-proofness (rather than 1-OCA-proofness). We do so to avoid clutter in the definitions, as in randomized mechanisms the winning coalition may very well necessarily include all bidders (as each has some fractional probability of winning).
\ We now consider a natural property for mechanisms:
\ Corollary 5.4. By Lemma 5.3, a DSIC+OCA-proof scale-invariant mechanism does not burn fees (i.e., its burn rule is the constant zero function), while from Lemma 3.5 we get that a DSIC+MMIC+OCAproof mechanism has payments equal to the burn in the single bidder case. Therefore, we must have 0 payments in the single bidder case, and so, in the single bidder case, the item is either always or never allocated.
\ Lemma 5.5. For a DSIC+MMIC+OCA-proof mechanism, if the item is always or never allocated in the single bidder case, the mechanism must be trivial.
\ 
\ Thus, as a direct result of Corollary 5.4 and Lemma 5.5, we have:
Corollary 5.6. There is no non-trivial scale-invariant DSIC+MMIC+OCA-proof mechanism.
\ The argument we use in Lemma 5.5 can be extended to allow us to also rule out the class of auctions that satisfy a property that we call constant total probability of allocation (CTPA), which is defined in Def. 5.7. This is an interesting class of auctions, as it includes all efficient auctions (that are part of the class of constant total probability 1 of allocation), including the first-price and second-price auctions.
\ 
\ 
\ 
\ and thus by the feasibility Eq. (1):
\ Notice that this is the left-hand side of the Lemma 5.12 where we consider the bids B · b, A · b. We can thus repeat the way we developed Eq. (14) (for the case of the bids A · b, A · b) and, by considering that the miner omits the bid B · b, get:
\ Furthermore, for the case of two bidders, we can show a useful upper and lower bound on how much the function should “favor” the higher bidder:
\ 
\ 
\ 
\
:::info Authors:
(1) Yotam Gafni, Weizmann Institute (yotam.gafni@gmail.com);
(2) Aviv Yaish, The Hebrew University, Jerusalem (aviv.yaish@mail.huji.ac.il).
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
You May Also Like

Crypto market crashes as Fear and Greed and Altcoin Season Index slips
